Seno hiperbólico

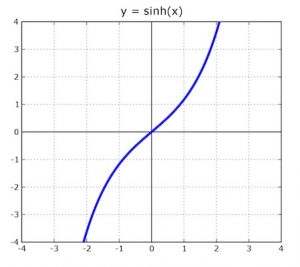
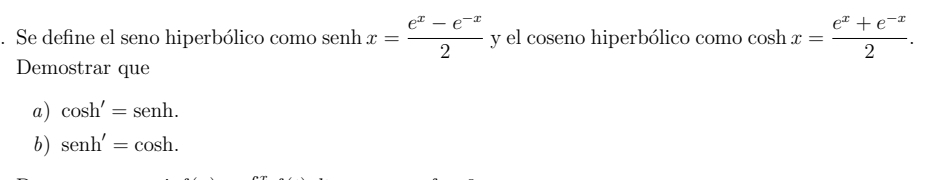El seno hiperbólico es una función real de variable real ${\displaystyle x}$, que se designa con ${\displaystyle \sinh(x)}$ está definida mediante la siguiente ecuación:

${\displaystyle \sinh(x)={\frac {e^{x}-e^{-x}}{2}}}$

^[1]​

donde ${\displaystyle e^{x}}$ es la función exponencial. Esta función, junto con el coseno hiperbólico y la tangente hiperbólica, conforman unas identidades como las trigonométricas circulares, pero con algunas excepciones. Entre ellas:

${\displaystyle {\cosh }^{2}{x}-{\sinh }^{2}{x}=1\,}$

${\displaystyle \tanh(x)={\frac {{\sinh }(x)}{\cosh(x)}}}$

Su relación con el seno está dada por:

${\displaystyle \sin(x)=-i\sinh(ix)}$

Propiedades

• Las funciones circulares seno y coseno están vinculadas con el círculo unitario de frontera x² y² = 1, mediante la ecuación sen² α cos²α =1; de igual manera, las hiperbólicas están vinculadas con la hipérbola x² - y² = 1, por medio de cosh² t -sinh² t = 1 donde t = 2 áreas de OCA, O = origen de coordenadas, A punto de la hipérbola, C vértice de la misma.^[2]​

• La función sinh(x) es una función impar, ya que para todo valor de x, se cumple que

${\displaystyle \sinh(-x)=-\sinh(x)}$

• La función senh x es creciente, puesto que su derivada es mayor que 0, en todo su campo de definición.^[3]​
• El punto (0; 0) es punto de inflexión, pues la segunda derivada varía de signo al pasar la función de valores negativos a valores positivos. Además es cóncava hacia abajo para x <0; y convexa hacia arriba para x > 0.^[4]​

Derivadas

${\displaystyle {{\mathrm {d} } \over {\mathrm {d} x}}{\sinh }(x)={\cosh }(x)}$

${\displaystyle {{\mathrm {d} } \over {\mathrm {d} x}}{\cosh }(x)={\sinh }(x)}$

Referencias y notas

Véase también

• Trigonometría
• Identidad trigonométrica
• Función hiperbólica
• Coseno hiperbólico

Enlaces externos

• Weisstein, Eric W. «Hyperbolic Sine». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.